- 벡터 : 숫자를 수직이나 수평으로 배열한 것
- 행렬 : 가로 세로로 표처럼 늘어 놓은 것
▼ 인덱스 값을 파이썬의 배열에 맞게 행렬도 0행 0열에서 시작됨

▼ 이런식으로 행렬의 인덱스 값을 줄 수 있음.
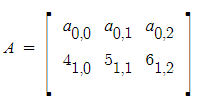
1. 행렬의 덧셈/뺄셈
: 두 행렬이 동일한 크기일때만 계산 가능 ▼ 요렇게
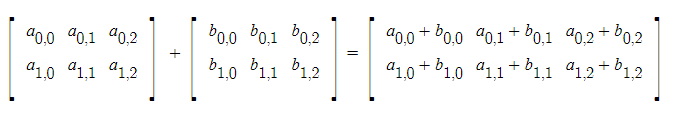
1-1. 파이썬에서 행렬의 덧셈과 뺄셈
- np.array(행렬값) 로 행렬을 정의해주고
- A + B or A - B 식의 사칙연산자를 활용하여 가능
2. 행렬의 곱
: https://dev-adela.tistory.com/61 게시글 보기 A.dot(B)형태까지 나와있음.
- 곱셈의 기호(*)를 사용하려면 대응하는 요소끼리 곱셈 수행. (덧셈/뺄셈 처럼)
- L X M 행렬과 M X N 행렬의 곱일 때의 공식

- 파이썬으로 계산할때는 A.dot(B)
* 정방행렬 : 가로와 세로 크기가 동일한 행렬 ex ) 2*2 / 3*3 / 6*6
- 정방행렬인 A가 B인 경우 A.dot(B) / B.dot(A) 둘다 계산 가능하지만 A.dot(B) != B.dot(A) 값은 다름.
▶ 곱할때 순서가 중요하다.
▷ A*B 일때는 똑같음
3. 단위행렬 : 정방 행렬일 때 대각선 성분이 1이고 그 외에는 0 인 행렬을 단위 행렬로 부름 (주로 I라고 지칭)
▶ 단위 행렬은 대각 성분이 1이기 때문에 다른 행렬을 곱해도 값이 변하지 않음.
4. 역행렬 : a의 역수는 1/a 이며 a^-1 로 나타낸다. 이거를 행렬에도 적용한 것
▶ 정방행렬인 경우에만 해당됨.

- 파이썬으로는 np.linalg.inv(A)로 역행렬을 구할 수 있음.
* 만약 ad-bc = 0 이 되는 행렬은 역행렬이 존재하지 않음.
5. 전치 : 행렬에도 벡터처럼 전치 T를 사용할 수 있음.
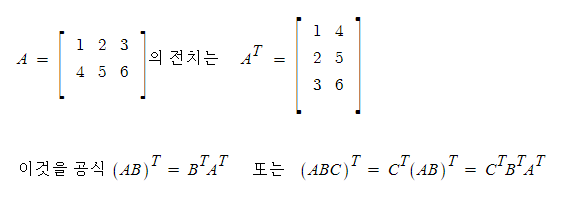
▶ 전치에 의해 인덱스 순서 바뀌니까 기억해두기
6. 행렬과 연립 방정식 : 연립 방정식을 하나의 행렬식으로 표현하고 행렬의 연산을 사용하여 답을 찾을 수 있음.
▶ y = 2x / y = -x +3 일경우,,,,,,, 행렬표기로 연립 방정식 풀어볼 수 있음. 손으로 풀어보기
7. 사상 : 그룹(벡터와 점)에서 그룹(벡터와 점)에 대응 관계를 제공하는 규칙, 행렬은 선형 사상으로 분류됨.
▶ 그러니까 어떤 점(좌표인 벡터, 행렬)을 다른 점으로 이동시키는 규칙
'머신러닝 > 개념익히기' 카테고리의 다른 글
| 학습/테스트데이터 - 홀드아웃, k-분할 교차검증, 과적합, 앙상블학습 (0) | 2023.07.17 |
|---|---|
| 지수함수와 로그함수 (0) | 2023.05.16 |
| 머신러닝에 필요한 수학 기본 - 합 / 곱 / 미분 (0) | 2023.05.15 |
| 벡터와 연산 (0) | 2023.05.10 |
| 3차원 그래프 그리기 (0) | 2023.05.09 |



