<모형평가 기준>
- 일반화의 가능성 : 같은 모집단 내 다른 데이터에 적용할 때도 안정적인 결과를 제공하는 것을 의미. 데이터를 확장하여 적용할 수 있는지에 대한 평가 기준
- 효율성 : 분류분석 모형이 얼마나 효과적으로 구축되었는지를 평가하는 것. 적은 입력 변수를 필요로 할수록 효율성이 높다
- 예측과 분류의 정확성 : 구축된 모형의 정확성 측면에서 평가하는 것으로 안정적이고 효율적인 모형을 구축하였다하더라도 실제 문제에 적용했을 때 정확하지 못한 결과만을 양산한다면 그 모형은 의미를 가질 수 없다.
<교차검증 Cross Validation>
- training, validation, test dataset으로 나누어 모형의 성과를 검증
- 과적합(Overfitting)문제를 해결하고 잘못된 가설을 가정하게 되는 제 2종 오류의 발생을 방지할 수 있음.
<교차검증 데이터 구분>
| 학습데이터 training data |
훈련용데이터, 분류기를 만들때, 데이터 마이닝의 모델을 학습할때 |
| 검증(검정)데이터 validation data |
과대추정, 과소추정을 미세조정하는데 활용. 분류기의 파라미터 값을 최적화하기 위해 사용하는 데이터 |
| 평가(시험)데이터 test data |
모형의 구축과 성관없는 외부데이터, 성능을 검증하기 위한 데이터 |
<홀드 아웃 Hold-Out>
- 원천 데이터를 랜덤하게 두 분류로 분리하여 교차검정을 실시하는 방법.
- 하나는 훈련용 / 하나는 검증용자료로
- 일반적으로 전체 데이터 중 70%는 훈련용, 나머지는 검증용
- 검증용은 성과 측정만을 위하여 사용
..... train_test_split..?
<k-fold 교차검증 k-fold cross validation>
- 주어진 데이터를 가지고 반복적으로 성과를 측정하여 그 결과를 평균한 것
- 동일한 k개의 하부집합(subset)으로 나누고 k번째 하부집합을 검증용 자료로 나머지 k-1개의 하부집합을 훈련용으로, k번 반복. 반복측정. 평균값 최종 평가. 일반적으로는 10-fold
<붓스트랩 Bootstrap>
- 단순 랜덤 복원추출 방법을 활용하여 동일한 표본의 크기의 표본을 여러개생성하는 복원추출법
- k-fold 교차검증과유사하나(평가반복하는점) 훈련용 자료를 반복 재산정한다는 점에서 다름
- 데이터 양이 크지 않을 때 좋음
- 샘플에 한 번도 선택되지 않은 확률은 36.8%가 해당됨
- 한번도 포함되지 않은 건 평가용으로
<ROC그래프, Receiver Operating Characteristic>
- 두 분류분석 모형의 결과를 시각화할 수 있음.
- x축에는 FP ratio(1-특이도), y축에는 민감도 나타내어 모형을 평가할수있따.
- 모두 1인 경우에는 모두 True로 분류된 경우. 모두 0인 경우는 False
> x축은 0, y축은 1의 값을 보여 AUC가 1로 도출되는 : 가장 이상적으로 완벽한 분류의 모형
- 밑부분 면적(Area Under the ROC curve, AUC)이 넓을수록 좋은 모형으로 평가. 0.5~1 범위를 가짐
<이익도표>
- 이익(Gain)은 목표 범주에 속하는 개체들이 각 등급에 얼마나 분포하고 있는지 나타내는 값
- 해당 등급에 따라 계산된 이익값을 누적으로 연결한 도표
- 분류분석 모형을 사용하여 분류된 관측치가 각 등급별로 얼마나 포함되는지를 나타내는 도표
<향상도 곡선 Lift Curve >
- 랜덤모델과 비교하여 해당 모델의 성과가 얼마나 향상되었는지를 각 등급별로 파악하는 그래프
- 상위등급에서 향상도가 매우크고 하위 등급으로 갈수록 감소하게 됨
> 일반적으로 예측력이 적절하지만 등급에 관계없이 향상도가 차이가 없으면 모형의 예측력이 좋지 않음
<로지스틱 회귀모형>
- 반응변수가 범주형인 경우에 적용되는 회귀분석 모형
- ex . 성공/실패, 흡연/비흡연, 생존/사망 등
- 2가지 범주로 되어있을 때 종속, 독립 변수간의 관계식을 이용하여 두 집단을 분류하고자 할 경우 사용되는 통계기법
<로짓변환>
- 반응변수가 범주형이므로 선형회귀 방식으로 fitting 하기 어렵다.
- 곡선에서 직선으로 fitting 하기 위해서 사용하는 것이 오즈에 로그를 취하는 로짓 변환
- y를 log(p/1-p)로 만드는 함수적 변환을 말함.
- 단순 로지스틱인 경우 로지스틱 회귀계수 β₁이 9보다 큰 경우에는 S자, 0보다 작은 경우에는 역 S자 모양을 가진다
> 이것이 시그모이드 함수
- 누적함수는 곧 성공의 확률, 이는 분류 목적으로 사용될 경우 0.5보다 크면 Y=1집단으로 작으면 Y=0집단으로 분류된다
<선형회귀분석 vs 로지스틱 회귀분석 비교>
| 일반선형 회귀분석 | 로지스틱 회귀분석 | |
| 종속변수 | 연속형 변수 | 이산형 변수 |
| 모형 탐색 방법 | 최소자승법 | 최대 우도법, 가중최소자승법 |
| 모형검정 | F-test, t-test | x²test |
<인공신경망의 종류 - 단층퍼셉트론(퍼셉트론)>
- 단층이라 입력층(input layer), 출력층(output layer)로만 구성된다. (히든레이어없다)
- 학습벡터or입력벡터가 입력되는 계층으로 입력된 데이터는 출력으로 전달되어 활성함수에 따라 값이 출력된다.
<인경신경망 - 가중치 weight>
- 퍼셉트론의 학습목표는 학습 벡터를 두 부류로 선형 분류하기 위한 선형 경계를 찾는 것이다. 가중치는 이러한 선형 경계의 방향성 또는 형태를 나타내는 값이다.
<인경신경망 - 바이어스 bias>
- 선형 경계의 절편을 나타내는 값으로써, 직선의 경우 y절편을 나타낸다.
*이해를 돕기 위해... net값 : 입력값/가중치의 곱을 모두합한 값.
*활성함수 : net값이 임계치보다 크면 1을 출력, 작으면 0을 출력
<단층 퍼셉트론의 XOR 문제>
- AND랑 OR 게이트는 직선을 그어 결괏값이 검은점을 구별할 수 있찌만 XOR은 안되었음.
>>> 이를 해결한 것이 다층 퍼셉트론
<다층퍼센트론>
- 하나 이상의 은닉층을 두어 비선형적으로 분리되는 데이터에 대해 학습이 가능한 퍼셉트론
- 목푯값과 출력값을 직접 비교가 불가능해서 이를 해결하기 위한 방법이 역전파 알고리즘.
<역전파 알고리즘 Backpropagation>
- 손실함수 : 신경망에 훈련데이터 x를 투입하고 실제출력, 기대출력간의 차이
> 훈련데이터를 이용해 가중치(w)와 바이어스(b)를 변화시키는 과정을 반복적으로 수행해 손실함수가 최소값이 되도록 하는것이 인공신경망의 학습목표
- 그래서 출력에서 생긴 오차를 반대로 입력 쪽으로 전파해서 가중치랑 바이어스를 갱신하게 되면 훈련데이터에 최적화된 가중치와 바이어스 값들을 얻을 수 있음
> 역전파 : 출력부터 반대방향으로 순차적으로 편미분을 수행해가면서 가중치와 바이어스를 갱신한다는 의미
<활성함수 Activation Function>
- 입력신호의 총합을 출력신호로 변환하는 함수
- 데이터를 비선형으로 변화하기 위해서 사용
- 시그모이드 함수 : 로지스틱함수(2개 분류)라고 함. 완만한 곡선 형태. 0~1 사이의 값 출력
> 소프트맥스 함수 : 목표값이 다 범주인 경우(3개 이상 분류). 입력받는 값을 정규화 한 후 0~1 출력. 노드의 출력값은 1
>ReLU함수 : 시그모이드 함수의 기울기 소실문제가 발견되면서 사용. 입력값이 0보다 작으면 0, 0보다 크면 입력값 그대로 출력
<경사하강법 Gradient Descent Method>
- 기울기를 구하며 최적의 가중치와 바이어스를 구하는 방법
- 일정 거리만큼 이동한다. (너무 크면 최적을 놓칠 수 있고, 너무 작으면 시간이 오래걸린다)
<기울기 소실문제 Vanishing Gradient Problem>
- 은닉층이 많아질수록 전달되는 오차가 크게 줄어 학습이 되지 않는 현상이 발생, 이를 기울기 소실문제
- 기울기가 거의 0이면 학습이 느려지고 학습이 다 되지 않은 상태에서 멈춤.
<의사결정나무 - 가지치기 Pruning>
- 모든 터미널 노드의 순도가 100%(불순도가 0)인 상태를 Full Tree
- 나무 크기 = 모형의 복잡도. 과적합 위험이 생길 수 있음.
- 타당성이 없는 규칙을 제거함으로써 과적합을 방지하고 적합한 수준에서 터미널 노드를 결합해주는 것
<정지규칙>
- 더이상 트리의 분리가 일어나지 않게 하는 규칙
- 하지 않으면 각 끝마디가 Full Tree까지 성장하므로 과적합 발생 가능
<의사결정나무 모형의 분류>
1. 분류 나무 classification tree
- 목표변수가 이산형인 경우
- 분류 기준값 선택 방법 : 카이제곱통계량의 p값, 지니지수(CART), 엔트로피 지수
* 지니지수 값이 클수록 이질적이며 순수도가 낮다고 볼 수 있음.
2. 회귀나무 regression tree
- 목표변수가 연속형인 경우
- F통계량의 p 값, 분산의 감소량(CART)
<의사결정나무의 장단점>
| 장점 | 구조단순 해석용이 유용한 입력 변수의 파악, 예측변수 간의 상호작용 및 비선형성을 고려하여 분석 가능 수학적 가정이 불필요한 비모수적 모형 계싼 비용이 낮아 대규모의 데이터 셋에서도 빠르게 연산 가능 수치형/범주형 변수 모두 사용가능 |
| 단점 | 분류 기준값의 경계선 부근의 자료값에 대해서는 오차가 큼 로지스틱회귀와 같이 각 예측변수의 효과 파악어려움 새로운 자료에 대한 예측 불안정 |
<앙상블 - 배깅>
- 원 데이터 집합으로부터 크기가 같은 표본을 여러번 단순임의복원추출하여 각 표본(붓스트랩표본)에 대해 분류를 생성한 후 그 결과를 앙상블하는 방법.
<앙상블 - 부스팅>
- 분류가 잘못된 데이터에 더 큰 가중을 주어 표본을 추출. (약한 분류기에 가중치를 부여하여 강한 분류기를 만듦)
<앙상블-랜덤포레스트>
- 배깅에 랜덤과정을 추가한 방법.
- 각 노드마다 모든 예측변수 안에서 최적의 분할(Split)을 선택하는 대신 예측 변수들을 임의로 추출하고, 추출된 변수 내에서 최적의 분할을 만들어 나가는 방법을 사용.
<계층적 군집의 거리측정 방법>
- 단일연결볍(최단연결법) : 한 군집의 점과 다른 군집의 점 사이의 가장 짧은 거리. 사슬모양으로 생길 수 있으며, 고립된 군집을 찾는데 중점
- 와드연결법 : 군집 내의 오차제곱합에 기초하여 군집을 수행한다.
- 완전연결법 / 평균연결법 / 중심연결법
<계층적 군집의 거리>
- 유클리드 거리 : 두 점간 차를 제곱하여 모두 더한 값의 양의 제곱근

- 맨하튼 거리 : 시가(cith-block)거리라고도 불림. 두 점간차의 절댓값을 합한 값
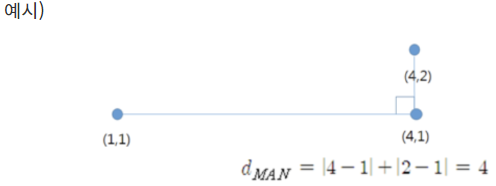
-마할라노비스 거리 : 변수의 표준화와 함께 변수 간의 상관성(분포형태)을 동시에 고려한 통계적 거리
- 민코프스키 거리/표준화거리
<비계층적 군집>
- k평균 군집(k-means clustering)
> 원하는 군집 수만큼 초기값을 지정하고, 각 개체를 가까운 초기값에 할당하여 군집을 형성한 뒤, 각 군집의 평균을 재계산하여 초기값을 갱신.
<실루엣 계수 Silhouette Coefficient>
- 각 데이터 포인트와 주위 데이터 포인트들과의 거리 계산을 통해 값을 구하며, 군집안에 있는 데이터들은 잘 모여있는지, 군집끼리는 잘 구분되는지 클러스터링을 평가하는 척도.
- 군집간의 거리가 얼마나 효율적으로 분리돼 있는지를 나타냄. (군집분석의 평가 지표)
<연관 규칙 Association rule>
- 장바구니 분석... 조건-결과식으로 표현되는 유용한 패턴. 패턴/규칙 발견해내는 것.
- 지지도/ 신뢰도/ 향상도가 측정지표
<apriori 알고리즘>
- 연관규칙의 대표적인 알고리즘. 데이터들에 대한 발생 빈도를 기반으로 각 데이터 간의 연관관계를 밝히기 위한 방법
- ex 소비자의 물건 구매 패턴
- 최소 지지도 설정 > 개별품목 중 최소 지지도를 넘는 모든 품목을 찾기 > 2에서 찾은 개별 품목만을 이용해 최소 지지도를 넘는 두 가지 품목 집합을 찾기 > 찾은 품목 집합을 결합하여 최소 지지도를 넘는 세가지 품목 집합 찾기 > 반복해서 최소 지지도가 넘는 빈발 품목 집합 찾기.
<FP-Growth알고리즘>
- FP-Tree라는 구조를 통해 최소 지지도를 만족하는 빈발아이템 집합을 추출할 수 있는 알고리즘
- 후보 빈발 아이템 집합을 생성하지 않아 apriori보다 속도가 빠르며 연산비용이 저렴
'ADsP' 카테고리의 다른 글
| ADsP 38회 합격 후기 (0) | 2023.11.15 |
|---|---|
| ADsP 3과목 데이터분석 정리 (1) (0) | 2023.08.18 |
| ADsP 2과목 데이터 분석 기획 정리 (0) | 2023.08.18 |
| ADsP 1과목 데이터 이해 정리 (1) | 2023.08.17 |
| ADsP 31회 기출문제 정리 (0) | 2023.08.16 |



