벡터와 연산
1.. 벡터란...............................................................................
몇 가지 숫자를 나란히 나타낸것... 크기와 방향을 가지고 있는.....
벡터를 표시할때는 소문자 볼드체로 함 a, b 요렇게 되어있으면 벡터!

- 세로 벡터 : 세로로 놓은 것
- 가로 백터 : 가로로 놓은 것. 옆으로 숫자 늘어놓은 것 리스트처럼
- 요소 : 벡터를 하나하나 구성하는 숫자
- 스칼라 : 일반적인 숫자의 묶음(집합), 소문자 이태릭체로 표시 a,b 요렇게!
- 전치 Transposition: T 라고 벡터 오른쪽 위에 적는것. 세로 벡터 > 가로 벡터로 / 가로벡터 > 세로 벡터로 변환한다는 의미
2. 파이썬으로 벡터 정의하기
- import numpy 한 후에
- numpy.array() 하면 됨
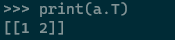
3. 세로 벡터 나타내기 (가로는 그냥 적으면 됨)

3-1 . 전치로 나타낼수도 있음 : 변수명.T 로
4. 벡터의 덧셈과 뺄셈
- 벡터의 덧셈/ 뺄셈은 각 요소를 더하거나 뺀다.

- 덧셈과 뺄셈을 그래프로 보기.
▶ 벡터를 화살표로 생각하면 a+b는 a와 b를 변으로 하는 평행 사변형의 대각선이다.
▶ 도형으로볼때 -b 는 b의 반대방향의 화살표이다. a + (-b)인셈.
▶ a의 x는 2라는 크기를 가지고 있고 세로는 1이라는 크기를 가지고 있음.
▷ 2라는 x값고 1이라는 y값의 길이 (빨간줄) 이 전체길이 ( 피타고라스의 정리로 구할수있음)
>> 여기서 보면 루트 5.

a = np.array([2,1])
b = np.array([1,3])
c = a+b
d = a-b
#a+b=c / a-b=d를 그래프로 그려보기
plt.xlim(-5,5)
plt.ylim(-5,5)
plt.xticks(ticks=np.arange(-5,5,1))
plt.yticks(ticks=np.arange(-5,5,1))
plt.arrow(0,0,a[0],a[1], head_width=.2, head_length=.2, color='red', length_includes_head=True)
plt.text(2,1, 'a')
plt.arrow(0,0,b[0],b[1], head_width=.2, head_length=.2, color='blue', length_includes_head=True)
plt.text(1,3, 'b')
plt.arrow(0,0,c[0],c[1], head_width=.2, head_length=.2, color='black', length_includes_head=True)
plt.text(3,4, 'c=a+b')
plt.arrow(0,0,d[0],d[1], head_width=.2, head_length=.2, color='green', length_includes_head=True)
plt.text(1,-2, 'd=a-b')
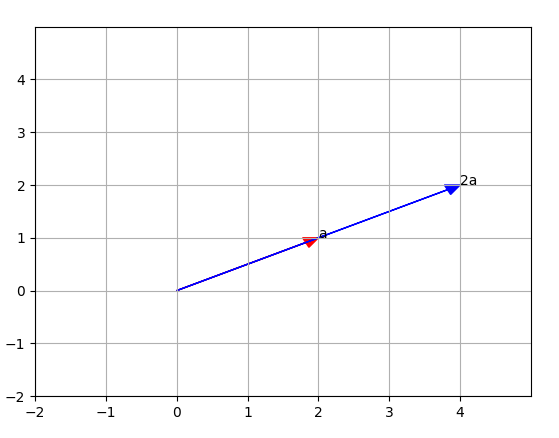
5. 스칼라의 곱셈
▼ 수식으로 봤을때. 스칼라에 벡터를 곱하면 스칼라 값이 벡터 요소 전체에 적용됨

▼ 도형으로 보면 벡터의 크기(길이)가 스칼라의 배가 됨.
6. 내적 : 벡터에서 곱셈 연산. 변수명1.dot(변수명2)
▶ c를 d로 투영한 벡터를 c' 로 해서 c'와 d의 길이를 곱해 합한 것.

▼ c' 의 크기 + d의 크기
▼ 두 벡터의 방향이 같더라도 한 쪽의 벡터 크기가 2배가 되면 내적도 2배가 됩니다.
▶ np.linalg.norm() : 벡터의 크기를 구할 수 있음.
